Introduction to slope: Definition, formula, and types

In algebra, the slope is used widely to measure the equation of the straight line and various algebraic expressions. The slope is very essential for solving the methods of the line’s equation. These methods are slope-intercept form, point-slope form, and two points intercept form.

In this post, we’ll learn about the definition, formula, and types of the slope along with a lot of examples.

What is the slope?

In algebra, a slope is used to measure the steepness of the line. The slope of each line remains the same across each point of the line. by using the coordinates points of the line, a slope can also describe the direction of the line.

The slope is generally a fraction of the change in the points of y coordinates by the change in the points of x coordinates. The change in x coordinates of the line is said to be the run. While the change in the y coordinates of the line is known as a rise.

So, the fraction result of rise and run is known as a slope. It is denoted by a lower case alphabet “m”. Mathematically, it can be written as:

Slope = m = change in y coordinates / change in x coordinates

Slope = m = rise / run

Slope = m = Δy/Δx 

Slope = m = y₂ – y₁ / x₂ – x₁

• In the above equation, y₁ & y₂ are the y coordinates of the line.
• x₁ & x₂ are the x coordinates of the line.
• m is the slope of the line.

Types of the slope of the line

In algebra, there are four main types of the slope of the line used frequently for the representation of the slope.

1. The positive slope of the line
2. The negative slope of the line
3. The zero slope of the line
4. The undefined slope of the line

Let’s discuss these types of slope briefly.

The positive slope of the line

When the object or a person follows a steep path to go upward from left to right is said to be the positive slope of the line. in this type of the slope, the values are positive. Following is a solved example of this type of slope.

Example

Find the slope of the line using the x and y coordinates of the line, (12, 2) and (15, 4).

Solution

Step 1: Determine the points of the line.

x₁ = 12, x₂ = 15, y₁ = 2, y₂ = 4

Step 2: Take the general formula of the slope of the line.

Slope of the line = m = Δy/Δx 

Step 3: Put the given points of the line in the formula.

Slope of the line = m = Δy/Δx = (y₂ – y₁) / (x₂ – x₁)

Slope of the line = m = (4 – 2) / (15 – 12)

Slope of the line = m = 2 / 3

Slope of the line = m = 0.6667

The negative slope of the line

When the object or a person follows a steep path to go down from left to right is said to be the negative slope of the line. In this type of slope, the values are negative. Following is a solved example of this type of slope.

Example

Find the slope of the line using the x and y coordinates of the line, (52, 32) and (26, 19).

Solution

Step 1: Determine the points of the line.

x₁ = 52, x₂ = 26, y₁ = -4, y₂ = 9

Step 2: Take the general formula of the slope of the line.

Slope of the line = m = Δy/Δx 

Step 3: Put the given points of the line in the formula.

Slope of the line = m = Δy/Δx = (y₂ – y₁) / (x₂ – x₁)

Slope of the line = m = (26 – 52) / (9 – (-4))

Slope of the line = m = (26 – 52) / (9 + 4)

Slope of the line = m = -26 / 13

Slope of the line = m = -2

You can also use a slope calculator to find the slope of the line by using the points of the line. follow the below steps to use this tool.

Step 1: Input the given points of the line.

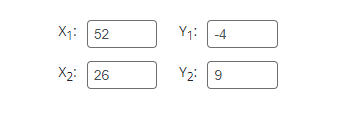
Step 2: Hit the calculate button.

Step 3: The result will show below the calculate button. Press show steps to view the solution with steps.

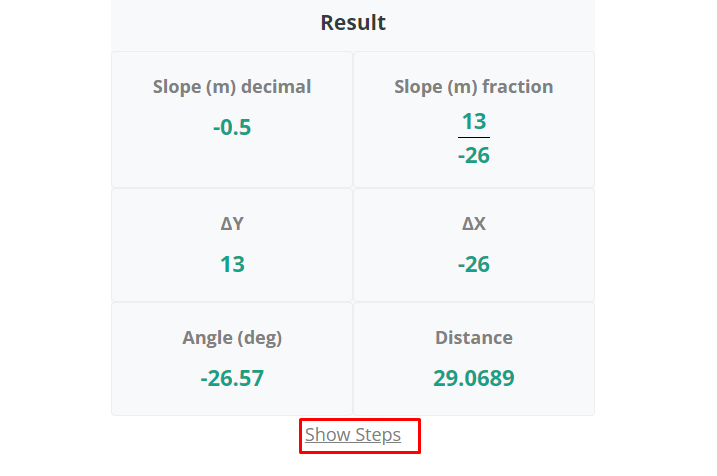
The zero slope of the line

When the object or a person follows a straight path without going upward or downward from left to right is said to be the zero slope of the line. In this type of slope, the values are 0. In other words, this type of slope deals with the x coordinates of the slope.

So, it is also known as a slope of a horizontal line. Following is a solved example of this type of slope.

Example

Find the slope of the line using the x and y coordinates of the line, (-32, 12) and (17, 12).

Solution

Step 1: Determine the points of the line.

x₁ = -32, x₂ = 17, y₁ = 12, y₂ = 12

Step 2: Take the general formula of the slope of the line.

Slope of the line = m = Δy/Δx 

Step 3: Put the given points of the line in the formula.

Slope of the line = m = Δy/Δx = y₂ – y₁ / x₂ – x₁

Slope of the line = m = (12 – 12) / (17 – (-32))

Slope of the line = m = (12 – 12) / (17 + 32)

Slope of the line = m = 0 / 49

Slope of the line = m = 0

The undefined slope of the line

When the object or a person follows a vertical path to go up or down without going from left to right is said to be the undefined slope of the line. In this type of slope, the values are at infinity. In other words, this type of slope deals with the y coordinates of the slope.

So, it is also known as a slope of a vertical line. Following is a solved example of this type of slope.

Example

Find the slope of the line using the x and y coordinates of the line, (-22, -32) and (-22, 2).

Solution

Step 1: Determine the points of the line.

x₁ = -22, x₂ = -22, y₁ = -32, y₂ = 2

Step 2: Take the general formula of the slope of the line.

Slope of the line = m = Δy/Δx 

Step 3: Put the given points of the line in the formula.

Slope of the line = m = Δy/Δx = (y₂ – y₁) / (x₂ – x₁)

Slope of the line = m = (2 – (-32)) / (-22 – (-22))

Slope of the line = m = (2 + 32) / (-22 + 22)

Slope of the line = m = 34 / 0

Slope of the line = m = undefined

Summary

In this post, we have learned about the definition, formula, and types of the slope with examples. Now you can solve any problem related to the slope of the line easily just by learning the basics of this post.