Most Difficult Areas in Mathematics and How to Learn Them (2024)

Reviewed by Soliu.

Several areas of mathematics are considered to be particularly difficult. The most difficult areas in mathematics include algebra, logic, calculus, mathematical physics, combinatorics, and number theory.

Math can be a tough subject, with many difficult areas to master. It requires a lot of brain power and perseverance to master the subject. From basic arithmetic to calculus and statistics, various topics can leave even the most dedicated students scratching their heads.

In this article, we’ll discuss the most difficult areas in mathematics and how to approach them with a positive mindset. Don’t worry – with the right strategies, you can tackle any math problem head-on!

Mathematics encompasses a wide range of topics, each with its unique challenges and learning approaches. Here’s an extensive overview of the most difficult areas in mathematics and strategies on how to learn them:

Most Difficult Areas in Mathematics

1. Algebra

When it comes to mathematics, algebra is often considered to be one of the most difficult areas to master. This is because algebra involves working with abstract concepts and manipulating symbols logically and rigorously. 

Students often struggle with the abstract nature of algebra and the numerous rules and procedures that need to be followed. In addition, algebra requires a strong foundation in basic math, such as addition, subtraction, division, and multiplication. 

The difficulty of algebra can be attributed to several specific areas of the subject. First is the concept of variables, which can confuse students who are used to working with specific numbers. In addition, algebraic equations often require the use of multiple steps, which can be challenging to follow for students who need to be better versed in the rules of algebra.

Furthermore, many algebraic problems involve word problems, which can be tricky to translate into mathematical equations. Finally, using exponents and radicals can be another difficulty for students. To make matters even more complicated, algebra is often a prerequisite for more advanced math courses such as calculus and statistics. 

For all these reasons, algebra is often considered one of the most challenging areas of mathematics.

2. Logic

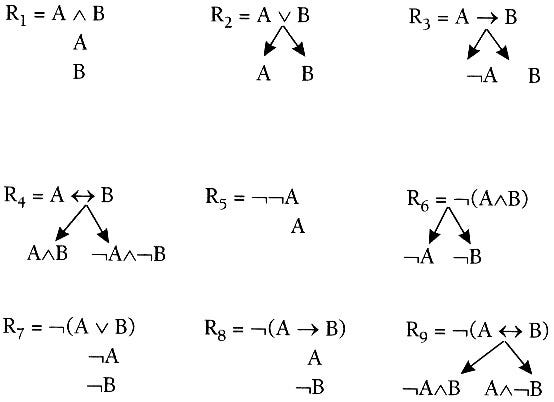
Logic, often called “mathematical reasoning,” is another area of mathematics that is particularly challenging. In logic, students must reason deductively and evaluate arguments using formal methods. 

These methods often require a significant amount of abstract thinking and can be challenging to grasp for students who are not accustomed to such rigorous thinking. Logic often deals with counterintuitive concepts that are difficult to visualize, such as set theory and mathematical induction. 

One challenging area of logic is the study of proofs. In proof-based logic, students must construct arguments demonstrating a statement’s truth or falsity. This requires an in-depth understanding of the underlying logical structure of the argument, as well as the ability to know and avoid logical fallacies. In addition, proofs often require sophisticated mathematical tools such as mathematical induction and the pigeonhole principle, making them even more challenging to grasp.

The foundation of mathematical logic and all of mathematics, logic deals with valid arguments and the principles of proof and evidence​​ , which is why it is one of the most challenging areas in mathematics. 

3. Calculus

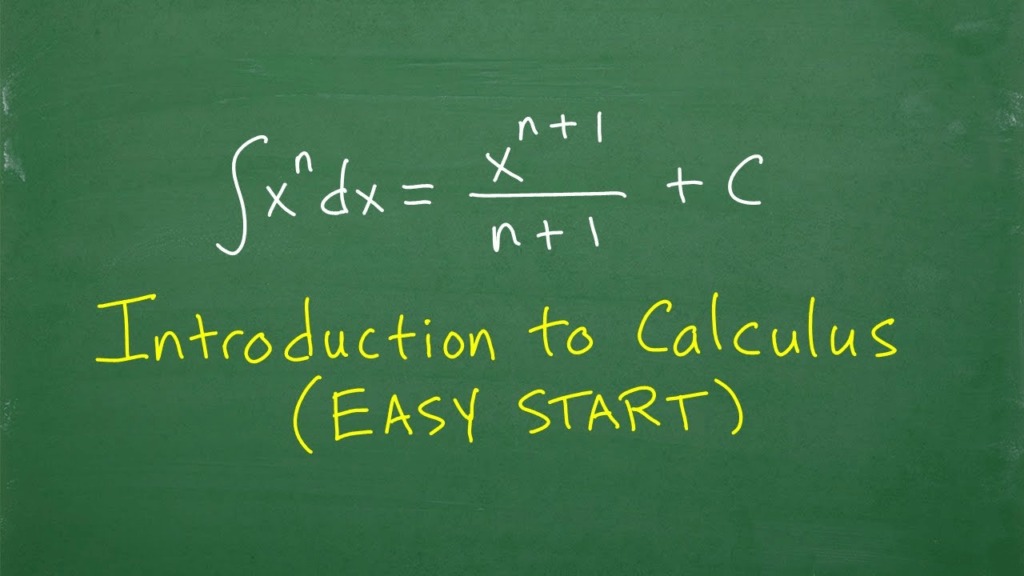
This field deals with rates of change (differential calculus) and the summation of infinite elements (integral calculus). It requires an understanding of integrals, derivatives, and limit functions​​. These concepts can be challenging to understand, especially for students without much experience with advanced mathematics. 

In addition, calculus is often used to solve complex physics and engineering problems, which can add to its difficulty. One specific area of calculus that can be especially difficult is differential equations. 

Differential equations involve finding solutions to equations that involve derivatives, and they are often used to model real-world phenomena. Some differential equations are unsolvable using standard methods and require numerical or computational techniques. 

Differential equations can be quite challenging, even for those with a strong calculus background. For many students, they are the most challenging aspect of calculus. Overall, calculus is a notoriously challenging subject, even for experienced mathematicians.

4. Geometry and Topology

Geometry deals with shapes, sizes, and volumes, while topology focuses on properties that remain constant through deformations like stretching and bending​​. These fields involve much abstract thinking and often require advanced mathematical techniques. 

Geometry and topology often intersect in the field of differential geometry. In differential geometry, one studies how geometric objects can be described using calculus and other mathematical tools. This area of mathematics is highly challenging, and many of its most famous problems remain unsolved. 

For example, the Poincaré conjecture, a famous unsolved problem in topology, has eluded mathematicians for over a century. Also, the Riemann hypothesis, one of the seven Millennium Prize Problems, is a major unsolved problem in differential geometry.

5. Combinatorics

Combinatorics is the study of how things can be combined or arranged, another field known for its difficulty. This area of mathematics involves many concepts, including graph theory, number theory, and probability.

Some famous unsolved combinator problems include the graph coloring problem, the Collatz conjecture, and the twin prime conjecture. These problems have stumped mathematicians for decades, and their solutions are considered some of the most challenging mathematics problems.

One famous problem in combinatorics is the P vs NP problem. This problem asks whether every problem whose solution can be verified quickly can also be solved quickly. It is considered one of the most challenging problems in computer science, and its solution would have significant implications for many fields. 

Some people believe that the P vs. NP problem is impossible to solve, but it has been studied by some of the greatest minds in mathematics and computer science. No one knows if a solution will ever be found, but the search continues.

6. Number Theory

Number theory is the study of the properties of integers and other whole numbers, and it is another area of mathematics known for its difficulty. This field has been around for centuries, producing some of the most beautiful and essential theorems in all of mathematics. 

Some of the most famous unsolved problems in number theory include Fermat’s Last Theorem, the Riemann hypothesis, and the Goldbach conjecture. These problems have stumped mathematicians for hundreds of years, and their solutions would be significant breakthroughs.

7. Dynamical Systems & Differential Equations

Dynamical systems and differential equations are closely related fields of mathematics that study how systems change over time. It involves mathematical expressions with unknown functions and their derivatives, often used to model real-world phenomena​​.

Dynamical systems and differential equations have many critical applications in physics, engineering, and other fields, but they can be complex and challenging to understand. Some famous unsolved problems in this area include the three-body problem and the Navier-Stokes equations.

The three-body problem is one of the most famous and challenging problems studying dynamical systems. This problem asks whether it is possible to precisely predict the future of a system with three or more bodies under the influence of gravity.

This problem has been studied for centuries, and it has important implications for the study of celestial mechanics and the planet orbits and other bodies in the solar system. The problem remains unsolved and is considered one of mathematics’s most significant unsolved problems.

8. Mathematical Physics

This field applies mathematics to solve physics problems and develop new mathematical methods and theories. Mathematical physics is a field that combines mathematics and physics to study physical systems. This field is notoriously difficult and requires understanding mathematics and physics. 

Some of this area’s most famous unsolved problems include the Navier-Stokes equations and the quantum measurement problem. The Navier-Stokes equations describe the flow of fluids and are one of the most important unsolved problems in mathematical physics.

The quantum measurement problem asks how the act of measurement affects the state of a quantum system, and it has profound implications for our understanding of the nature of reality.

This problem has stumped physicists and mathematicians for decades and remains one of the most challenging areas in mathematics and modern physics.

9. Computation

Computational mathematics studies how computers can be used to solve mathematical problems. This field is complex because it requires knowledge of both mathematics and computer science. It encompasses computer science, algorithms, scientific computing, and data structures.

One very challenging area of computational mathematics is the field of artificial intelligence. AI researchers are developing algorithms that can solve problems and make decisions similar to those made by humans. However, creating brilliant machines that adapt to new situations is still very difficult. 

Some researchers believe that true AI is impossible to achieve. In contrast, others believe it is only a matter of time before we can create AI indistinguishable from human intelligence. Do you think we will ever achieve true AI?

10. Information Theory and Signal Processing

Information theory quantifies data, while signal processing involves manipulating and interpreting various signals like sound and images​​. Information theory and signal processing are two closely related areas of maths that deal with information representation, transmission, and processing. 

These fields are challenging because they require a deep understanding of probability theory, statistics, and linear algebra. Signal processing is also a very applied field, which means that many problems are particular and complex. 

Learning Strategies for Difficult Mathematics Topics

Consistent Practice Routine: Regular practice is crucial for retaining complex mathematical concepts. A set amount of problems each session can make challenging material more familiar and less intimidating​​.

Ask Questions: Engaging actively in class by asking questions enhances understanding and retention. Preparing questions from homework problems can be incredibly effective​​.

Join a Math Study Group: Learning in groups allows for exchanging different techniques and mutual support, which can be particularly helpful in understanding complex concepts​​. Working in groups allows students to view problems differently and promotes out-of-the-box thinking.

Seeking Help from Teachers or Tutors: Personalized guidance from tutors or teachers can provide step-by-step problem-solving methods and help understand complex topics​​.

Confident and Positive Attitude: Approaching math confidently and focusing on small victories can significantly improve learning outcomes in challenging areas​​.

Explicit Instruction: Starting lessons with clear, direct instruction and using visual aids can help students grasp complex concepts more quickly​​.

Utilizing Math Vocabulary: Describing mathematical concepts in various ways and incorporating them into everyday language can enhance understanding​​.

Incorporating Meaningful Homework: Including games and practical applications in homework can make learning more engaging and effective​​.

Puzzle Piece Instruction: Breaking problems into smaller parts and collaborating to solve them can help understand complex topics​​.

Verbalizing Problems: Discussing and verbalizing math problems encourages more profound understanding and allows students to ask questions and explore concepts more thoroughly​​.

Reflection Time: Allowing time for group and individual reflection helps in processing and understanding the material covered​​.

Making Math Fun: Using games and interactive activities can make learning even the most challenging math topics enjoyable and effective​​.

In summary, mastering difficult areas mathematics requires consistent practice, active engagement, seeking help when needed, and employing various learning strategies. Each topic presents unique challenges but can be effectively learned and understood with the right approach.

Tips to learn difficult topics in mathematics:

Faqs

What is the hardest part of mathematics?

Identifying the most challenging part of mathematics is subjective and based on individual strengths and weaknesses. However, some of the most challenging areas include Algebra, Logic, Calculus, Geometry and Topology, Combinatory, Number Theory, Computation, Dynamical Systems and Differential Equations, Mathematical Physics, and Information Theory and Signal Processing.

What is the most difficult area in math?

As mentioned above, some of the most difficult areas include Algebra, Calculus, and Number Theory, among others.

Which branch of mathematics is the most difficult?

The branches of Mathematics considered the most difficult include Higher Algebra, Advanced Calculus, and Complex Number Theory. You can add yours. 

What are the seven hardest math Problems?

7 Hardest Math Problems include the Millennium Problems, as presented by the Clay Mathematics Institute, include six unsolved problems: P vs. NP Problem, the Riemann Hypothesis, the Yang–Mills and Mass Gap, the Navier–Stokes Equation, the Hodge Conjecture, and the Birch and Swinnerton-Dyer Conjecture. The seventh, the Poincaré Conjecture, was solved by Grigori Perelman.

What is the easiest topic in maths?

Easier topics in mathematics are often those introduced at the elementary level, such as basic Algebra, Geometry, Heron’s Formula, Pythagorean Theorem, Trigonometry, Circles, Profit and Loss, Percentages, Statistics, Probability Theory, and Fractions and Decimals.

What is the highest level in math?

The highest level in mathematics typically involves advanced theoretical research in fields like Algebraic Geometry, Complex Analysis, Topology, and Number Theory, often pursued in doctoral studies and postdoctoral research.

What is the oldest branch of math?

The oldest Branch of Math can be traced back to prehistoric times with the use of geometric patterns and the quantification of time, as seen with artifacts like the Lebombo bone (approx. 35,000 BC to 20,000 BC) and the Ishango bone (c. 20,000 BC). Early developments in Mesopotamia (c. 3400 BC) included numeral systems, weights, and measures.

Which is more complicated: Algebra or calculus?

Algebra vs. Calculus: Calculus is generally considered harder than Algebra, and that’s it for me. Calculus is more complex and builds upon knowledge acquired in Algebra, Geometry, and Trigonometry. Its difficulty often arises from the need for a strong foundation in these preceding subjects. Let me know what you think about this in the comments box.

Conclusion 

So, we’ve discussed some of the most difficult areas in mathematics and offered tips on tackling them. Now, it’s up to you to put these tips into practice and tackle the challenges head-on. Be patient, take things one step at a time, and seek help when needed. 

Anyone with the right mindset and determination can learn mathematics. Don’t be afraid to ask for help, and keep practicing – you’ll be amazed at what you can achieve!